Reshaping a matrix

874th solved. Goal is to transform a matrix AxB into another one CxD. First if the dimensions don't match (A*B != C*D) then you just return the original matrix. Otherwise you do a pass on CxD and keep a row and col variables tracking the first matrix, changing them accordingly. Code is down below, cheers, ACC.

Oh, and here is me in the ACM collegiate contest, some time in a different century...

Reshape the Matrix - LeetCode

566. Reshape the Matrix

Easy

In MATLAB, there is a handy function called reshape which can reshape an m x n matrix into a new one with a different size r x c keeping its original data.

You are given an m x n matrix mat and two integers r and c representing the row number and column number of the wanted reshaped matrix.

The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.

If the reshape operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.

 

Example 1:

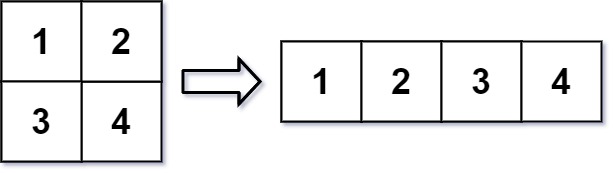
Input: mat = [[1,2],[3,4]], r = 1, c = 4
Output: [[1,2,3,4]]

Example 2:

Input: mat = [[1,2],[3,4]], r = 2, c = 4
Output: [[1,2],[3,4]]

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• -1000 <= mat[i][j] <= 1000
• 1 <= r, c <= 300

public int[][] MatrixReshape(int[][] mat, int r, int c)
{
    if (mat.Length * mat[0].Length != r * c) return mat;

    int[][] retVal = new int[r][];
    for (int i = 0; i < r; i++) retVal[i] = new int[c];

    int row = 0;
    int col = 0;
    for (int i = 0; i < r; i++)
    {
        for (int j = 0; j < c; j++)
        {
            retVal[i][j] = mat[row][col];
            col++;
            if (col == mat[0].Length)
            {
                row++;
                col = 0;
            }
        }
    }

    return retVal;
}