Classic Dynamic Programming II

Hard Leetcode problems often require a DP solution. This one is no different. The DP min formula is actually fairly simple, the complication is: do we simulate the train going thru the regular path first, or going thru the expression path first? Answer: try both, pick the min from them. Code is down below, cheers, ACC.

Minimum Costs Using the Train Line - LeetCode

2361. Minimum Costs Using the Train Line

Hard

A train line going through a city has two routes, the regular route and the express route. Both routes go through the same n + 1 stops labeled from 0 to n. Initially, you start on the regular route at stop 0.

You are given two 1-indexed integer arrays regular and express, both of length n. regular[i] describes the cost it takes to go from stop i - 1 to stop i using the regular route, and express[i] describes the cost it takes to go from stop i - 1 to stop i using the express route.

You are also given an integer expressCost which represents the cost to transfer from the regular route to the express route.

Note that:

• There is no cost to transfer from the express route back to the regular route.
• You pay expressCost every time you transfer from the regular route to the express route.
• There is no extra cost to stay on the express route.

Return a 1-indexed array costs of length n, where costs[i] is the minimum cost to reach stop i from stop 0.

Note that a stop can be counted as reached from either route.

 

Example 1:

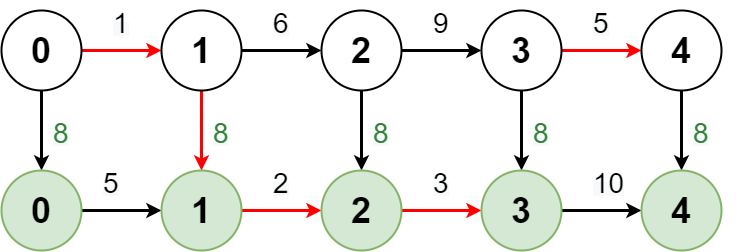
Input: regular = [1,6,9,5], express = [5,2,3,10], expressCost = 8
Output: [1,7,14,19]
Explanation: The diagram above shows how to reach stop 4 from stop 0 with minimum cost.
- Take the regular route from stop 0 to stop 1, costing 1.
- Take the express route from stop 1 to stop 2, costing 8 + 2 = 10.
- Take the express route from stop 2 to stop 3, costing 3.
- Take the regular route from stop 3 to stop 4, costing 5.
The total cost is 1 + 10 + 3 + 5 = 19.
Note that a different route could be taken to reach the other stops with minimum cost.

Example 2:

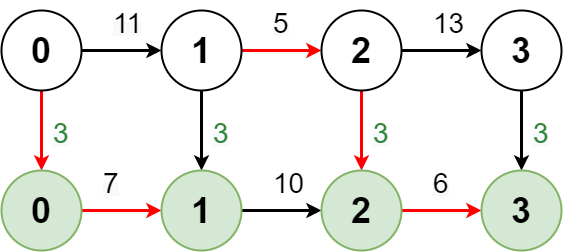
Input: regular = [11,5,13], express = [7,10,6], expressCost = 3
Output: [10,15,24]
Explanation: The diagram above shows how to reach stop 3 from stop 0 with minimum cost.
- Take the express route from stop 0 to stop 1, costing 3 + 7 = 10.
- Take the regular route from stop 1 to stop 2, costing 5.
- Take the express route from stop 2 to stop 3, costing 3 + 6 = 9.
The total cost is 10 + 5 + 9 = 24.
Note that the expressCost is paid again to transfer back to the express route.

 

Constraints:

• n == regular.length == express.length
• 1 <= n <= 105
• 1 <= regular[i], express[i], expressCost <= 105

Accepted

229

Submissions

262

public long[] MinimumCosts(int[] regular, int[] express, int expressCost)
{
    long[] minRegular = new long[regular.Length + 1];
    long[] minExpress = new long[express.Length + 1];

    minRegular[0] = 0;
    minExpress[0] = expressCost;

    for (int i = 1; i < minRegular.Length; i++)
    {
        minRegular[i] = 100000L * 100000 + 7;
        minExpress[i] = 100000L * 100000 + 7;
    }

    long[] retVal = new long[regular.Length];
    for (int i = 1; i < minRegular.Length; i++)
    {
        //Case 1: assume the path jumps from i-1 to i thru regular path first
        long tempMinRegular1 = Math.Min(minRegular[i - 1] + regular[i - 1], minExpress[i]);
        long tempMinExpress1 = Math.Min(minExpress[i - 1] + express[i - 1], tempMinRegular1 + expressCost);

        //Case 2: assume the path jumps from i-1 to i thru express path first
        long tempMinExpress2 = Math.Min(minExpress[i - 1] + express[i - 1], minRegular[i] + expressCost);
        long tempMinRegular2 = Math.Min(minRegular[i - 1] + regular[i - 1], tempMinExpress2);

        //Get the best out of case 1 and case 2 for both regular and express
        minRegular[i] = Math.Min(tempMinRegular1, tempMinRegular2);
        minExpress[i] = Math.Min(tempMinExpress1, tempMinExpress2);

        //Get the best out of regular and express
        retVal[i - 1] = Math.Min(minRegular[i], minExpress[i]);
    }

    return retVal;
}