Four HashTables

Using four HashTables to solve this problem, two for rows, two for columns. Two passes in the matrix, for a time complexity of O(n*m). Code is down below, cheers, ACC.

Difference Between Ones and Zeros in Row and Column - LeetCode

2482. Difference Between Ones and Zeros in Row and Column

Medium

You are given a 0-indexed m x n binary matrix grid.

A 0-indexed m x n difference matrix diff is created with the following procedure:

• Let the number of ones in the ith row be onesRowi.
• Let the number of ones in the jth column be onesColj.
• Let the number of zeros in the ith row be zerosRowi.
• Let the number of zeros in the jth column be zerosColj.
• diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj

Return the difference matrix diff.

 

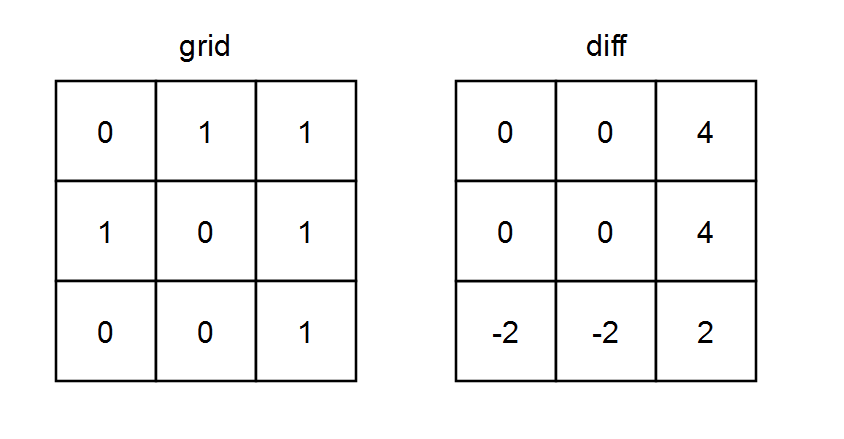
Example 1:

Input: grid = [[0,1,1],[1,0,1],[0,0,1]]
Output: [[0,0,4],[0,0,4],[-2,-2,2]]
Explanation:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 2 + 1 - 1 - 2 = 0 
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 2 + 1 - 1 - 2 = 0 
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 2 + 3 - 1 - 0 = 4 
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 2 + 1 - 1 - 2 = 0 
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 2 + 1 - 1 - 2 = 0 
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 2 + 3 - 1 - 0 = 4 
- diff[2][0] = onesRow2 + onesCol0 - zerosRow2 - zerosCol0 = 1 + 1 - 2 - 2 = -2
- diff[2][1] = onesRow2 + onesCol1 - zerosRow2 - zerosCol1 = 1 + 1 - 2 - 2 = -2
- diff[2][2] = onesRow2 + onesCol2 - zerosRow2 - zerosCol2 = 1 + 3 - 2 - 0 = 2

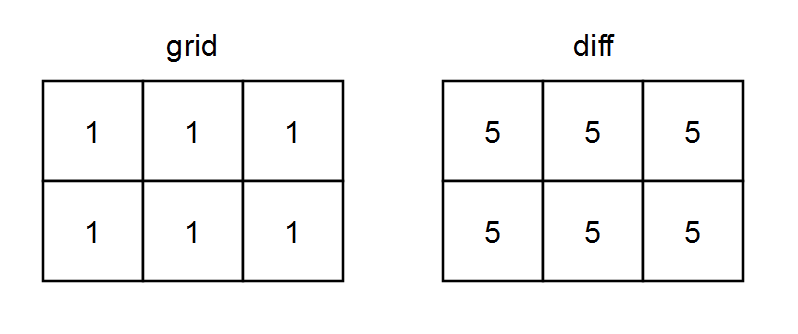
Example 2:

Input: grid = [[1,1,1],[1,1,1]]
Output: [[5,5,5],[5,5,5]]
Explanation:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• grid[i][j] is either 0 or 1.

public int[][] OnesMinusZeros(int[][] grid)
{
    Hashtable rowOnes = new Hashtable();
    Hashtable rowZeroes = new Hashtable();
    Hashtable colOnes = new Hashtable();
    Hashtable colZeroes = new Hashtable();

    for (int r = 0; r < grid.Length; r++)
    {
        for (int c = 0; c < grid[r].Length; c++)
        {
            if (grid[r][c] == 1)
            {
                if (!rowOnes.ContainsKey(r)) rowOnes.Add(r, 0);
                rowOnes[r] = (int)rowOnes[r] + 1;
                if (!colOnes.ContainsKey(c)) colOnes.Add(c, 0);
                colOnes[c] = (int)colOnes[c] + 1;
            }
            else
            {
                if (!rowZeroes.ContainsKey(r)) rowZeroes.Add(r, 0);
                rowZeroes[r] = (int)rowZeroes[r] + 1;
                if (!colZeroes.ContainsKey(c)) colZeroes.Add(c, 0);
                colZeroes[c] = (int)colZeroes[c] + 1;
            }
        }
    }

    for (int r = 0; r < grid.Length; r++)
    {
        for (int c = 0; c < grid[r].Length; c++)
        {
            grid[r][c] = (rowOnes.ContainsKey(r) ? (int)rowOnes[r] : 0) + 
                            (colOnes.ContainsKey(c) ? (int)colOnes[c] : 0) - 
                            (rowZeroes.ContainsKey(r) ? (int)rowZeroes[r] : 0) - 
                            (colZeroes.ContainsKey(c) ? (int)colZeroes[c] : 0);
        }
    }

    return grid;
}