Working around Dynamic Programming

This problem is a classic DP problem, and the hints confirm it. Couldn't solve it using DP, and the brute-force DFS approach was leading to TLE. So... decided to try to work around it. 
The heuristic used was simple: if we try way too many interactions (say 10x100x100), then we'll assume that there is no solution. It means that we have tried 10 times more cells that exists on the board. It worked. Sometimes achieving the goals requires creative and shameless approaches. Code is down below, cheers, ACC.

Check if There is a Path With Equal Number of 0's And 1's - LeetCode

2510. Check if There is a Path With Equal Number of 0's And 1's

Medium

You are given a 0-indexed m x n binary matrix grid. You can move from a cell (row, col) to any of the cells (row + 1, col) or (row, col + 1).

Return true if there is a path from (0, 0) to (m - 1, n - 1) that visits an equal number of 0's and 1's. Otherwise return false.

 

Example 1:

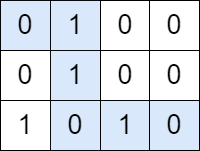
Input: grid = [[0,1,0,0],[0,1,0,0],[1,0,1,0]]
Output: true
Explanation: The path colored in blue in the above diagram is a valid path because we have 3 cells with a value of 1 and 3 with a value of 0. Since there is a valid path, we return true.

Example 2:

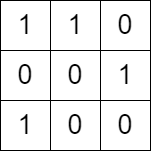
Input: grid = [[1,1,0],[0,0,1],[1,0,0]]
Output: false
Explanation: There is no path in this grid with an equal number of 0's and 1's.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 100
• grid[i][j] is either 0 or 1.

Accepted

206

Submissions

304

public bool IsThereAPath(int[][] grid)
{
    int interactions = 0;
    return IsThereAPath(grid, 0, 0, 0, 0, ref interactions, 10000000);
}

private bool IsThereAPath(int[][] grid,
                            int row,
                            int col,
                            int numberOnes,
                            int numberZeroes,
                            ref int interactions,
                            int MAX)
{
    if (interactions >= MAX) return false;

    if (row >= grid.Length || col >= grid[0].Length) return false;

    numberOnes = (grid[row][col] == 1) ? numberOnes + 1 : numberOnes;
    numberZeroes = (grid[row][col] == 0) ? numberZeroes + 1 : numberZeroes;

    if (row == grid.Length - 1 && col == grid[row].Length - 1) return numberOnes == numberZeroes;

    int rowsLeft = grid.Length - row - 1;
    int colsLeft = grid[0].Length - col - 1;

    if (Math.Abs(numberOnes - numberZeroes) > rowsLeft + colsLeft) return false;

    interactions++;
    if (IsThereAPath(grid, row, col + 1, numberOnes, numberZeroes, ref interactions, MAX)) return true;
    interactions++;
    return IsThereAPath(grid, row + 1, col, numberOnes, numberZeroes, ref interactions, MAX);
}