Classic Dynamic Programming V

Another classic DP, this time a standard traversal in a graph. Just need to follow the rules to move from column c-1 to c. Also, need to ensure that we can only proceed from where we are at if there has been a valid path to here. That's why there is a bit of calculation first to get the proper values v1,v2,v3, but after that it is pretty straightforward. Code is down below, cheers, ACC.

Maximum Number of Moves in a Grid - LeetCode

2684. Maximum Number of Moves in a Grid

Medium

You are given a 0-indexed m x n matrix grid consisting of positive integers.

You can start at any cell in the first column of the matrix, and traverse the grid in the following way:

• From a cell (row, col), you can move to any of the cells: (row - 1, col + 1), (row, col + 1) and (row + 1, col + 1) such that the value of the cell you move to, should be strictly bigger than the value of the current cell.

Return the maximum number of moves that you can perform.

 

Example 1:

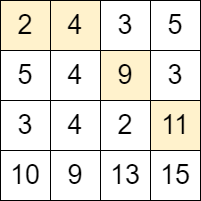
Input: grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
Output: 3
Explanation: We can start at the cell (0, 0) and make the following moves:
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
It can be shown that it is the maximum number of moves that can be made.

Example 2:

Input: grid = [[3,2,4],[2,1,9],[1,1,7]]
Output: 0
Explanation: Starting from any cell in the first column we cannot perform any moves.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 106

public int MaxMoves(int[][] grid)
{
    int[][] dp = new int[grid.Length][];
    for (int r = 0; r < grid.Length; r++)
        dp[r] = new int[grid[r].Length];

    int retVal = 0;
    for (int c = 1; c < grid[0].Length; c++)
    {
        for (int r = 0; r < grid.Length; r++)
        {
            int v1 = 0;
            if (r - 1 >= 0 && (c - 1 == 0 || dp[r - 1][c - 1] > 0) && grid[r - 1][c - 1] < grid[r][c])
                v1 = dp[r - 1][c - 1] + 1;

            int v2 = 0;
            if ((c - 1 == 0 || dp[r][c - 1] > 0) && grid[r][c - 1] < grid[r][c])
                v2 = dp[r][c - 1] + 1;

            int v3 = 0;
            if (r + 1 < grid.Length && (c - 1 == 0 || dp[r + 1][c - 1] > 0) && grid[r + 1][c - 1] < grid[r][c])
                v3 = dp[r + 1][c - 1] + 1;

            int[] arr = { v1, v2, v3 };
            foreach (int v in arr)
                dp[r][c] = Math.Max(dp[r][c], v);

            retVal = Math.Max(retVal, dp[r][c]);
        }
    }

    return retVal;
}