Marking Edges and Nodes in a graph

Many times we're accustomed to counting or marking the number of nodes in a graph. But this problem not only requires you to do so for the Nodes, but also for the Edges. In an indirect graph, the search can lead to edges that are adjacent to an already-visited node. The best way that I find to deal with this situation is to have another hash table, this time for the edges, and mark them using the following approach:

key = (large number) * Max(a,b) + Min(a,b)

You can see this approach in use here. Once you count the number of edges and nodes in a connected subgraph, it becomes straightforward to determine whether the subgraph is complete or not. Code is down below, cheers, ACC.

Count the Number of Complete Components - LeetCode

2685. Count the Number of Complete Components

Medium

You are given an integer n. There is an undirected graph with n vertices, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting vertices ai and bi.

Return the number of complete connected components of the graph.

A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.

A connected component is said to be complete if there exists an edge between every pair of its vertices.

 

Example 1:

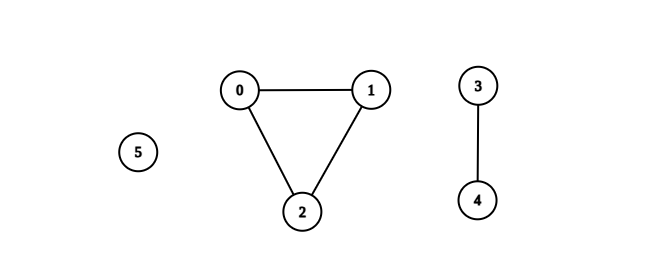
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
Output: 3
Explanation: From the picture above, one can see that all of the components of this graph are complete.

Example 2:

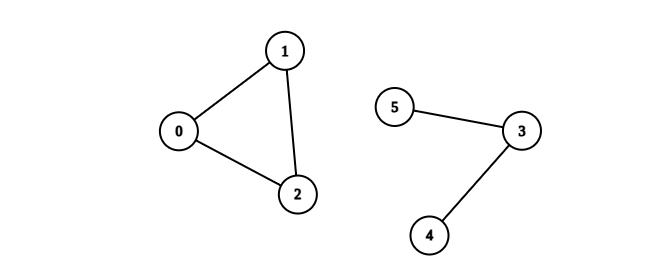
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
Output: 1
Explanation: The component containing vertices 0, 1, and 2 is complete since there is an edge between every pair of two vertices. On the other hand, the component containing vertices 3, 4, and 5 is not complete since there is no edge between vertices 4 and 5. Thus, the number of complete components in this graph is 1.

 

Constraints:

• 1 <= n <= 50
• 0 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi
• There are no repeated edges.

private Hashtable CreateGraphFromEdges(int[][] edges)
{
    Hashtable graph = new Hashtable();
    for (int i = 0; i < edges.Length; i++)
    {
        for (int j = 0; j < edges[i].Length; j++)
        {
            int from = edges[i][j];
            int to = edges[i][(j + 1) % edges[i].Length];

            if (!graph.ContainsKey(from)) graph.Add(from, new Hashtable());
            Hashtable connections = (Hashtable)graph[from];
            if (!connections.ContainsKey(to)) connections.Add(to, true);
        }
    }
    return graph;
}

private void MarkGraph(Hashtable graph,
                        int index,
                        Hashtable visitedNodes,
                        Hashtable visitedEdges)
{
    if (!visitedNodes.ContainsKey(index))
        visitedNodes.Add(index, true);

    if (graph.ContainsKey(index))
    {
        Hashtable connections = (Hashtable)graph[index];
        foreach(int connection in connections.Keys)
        {
            int key = 57 * Math.Max(connection, index) + Math.Min(connection, index);
            if (!visitedEdges.ContainsKey(key)) visitedEdges.Add(key, true);
            if (!visitedNodes.ContainsKey(connection))
            {
                visitedNodes.Add(connection, true);
                MarkGraph(graph, connection, visitedNodes, visitedEdges);
            }
        }
    }
}

public int CountCompleteComponents(int n, int[][] edges)
{
    Hashtable graph = CreateGraphFromEdges(edges);
    Hashtable visited = new Hashtable();

    int retVal = 0;
    for (int i = 0; i < n; i++)
    {
        if (!visited.ContainsKey(i))
        {
            Hashtable visitedNodes = new Hashtable();
            Hashtable visitedEdges = new Hashtable();
            MarkGraph(graph, i, visitedNodes, visitedEdges);
            if (visitedEdges.Count == (visitedNodes.Count * (visitedNodes.Count - 1) / 2)) retVal++;

            foreach (int key in visitedNodes.Keys)
                if (!visited.ContainsKey(key)) visited.Add(key, true);
        }
    }

    return retVal;
}