Classic Dynamic Programming VII

This is a simple one where you don't even need to allocate extra memory - use the grid itself as the DP storage, assuming that you don't need to keep the elements of grid intact. Code is down below, cheers, ACC.

Count Submatrices with Top-Left Element and Sum Less Than k - LeetCode

You are given a 0-indexed integer matrix grid and an integer k.

Return the number of 

submatrices

 that contain the top-left element of the grid, and have a sum less than or equal to k.

 

Example 1:

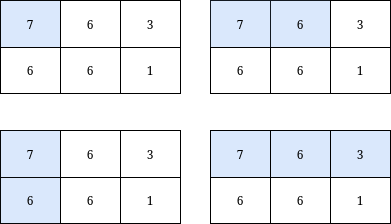
Input: grid = [[7,6,3],[6,6,1]], k = 18
Output: 4
Explanation: There are only 4 submatrices, shown in the image above, that contain the top-left element of grid, and have a sum less than or equal to 18.

Example 2:

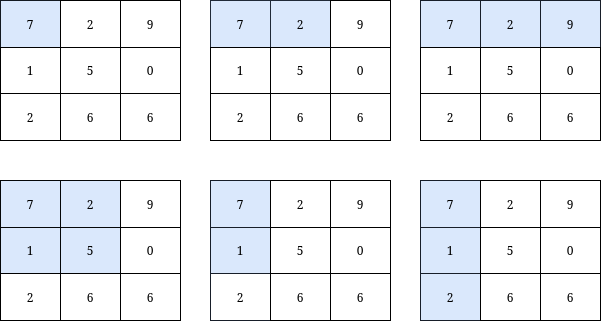
Input: grid = [[7,2,9],[1,5,0],[2,6,6]], k = 20
Output: 6
Explanation: There are only 6 submatrices, shown in the image above, that contain the top-left element of grid, and have a sum less than or equal to 20.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= n, m <= 1000
• 0 <= grid[i][j] <= 1000
• 1 <= k <= 109

public int CountSubmatrices(int[][] grid, int k)
{
    int retVal = 0;

    for (int r = 0; r < grid.Length; r++)
    {
        for (int c = 0; c < grid[r].Length; c++)
        {
            if (r - 1 >= 0 && c - 1 >= 0)
            {
                grid[r][c] += grid[r - 1][c] + grid[r][c - 1] - grid[r - 1][c - 1];
            }
            else if (r - 1 >= 0)
            {
                grid[r][c] += grid[r - 1][c];
            }
            else if (c - 1 >= 0)
            {
                grid[r][c] += grid[r][c - 1];
            }

            if (grid[r][c] <= k) retVal++;
        }
    }

    return retVal;
}