From N^2 to N
Problem is here: https://leetcode.com/problems/maximum-difference-between-node-and-ancestor/
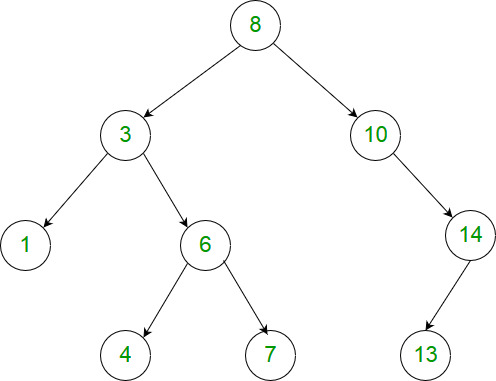
An N^2 approach seems at a glance to be the most logical approach: for each node, do a DFS traversal, calculate the value |node.val - eachChild|, and keep track of the max. Given than N = 5000, this might work (total 25,000,000 iterations..). However, there is a way to do it in N:
If you think about the problem carefully, you'll realize that inevitably your answer will be of the form |A-B| where either A is the largest value in your tree, or B is the smallest. To prove this lemma, suppose that your solution is |A-B| and suppose that you have found another node C such that C<B. Well, |A-C| will be clearly be larger than |A-B|, hence |A-B| cannot be your solution.
That being said, you can do a post-order DFS keeping track of the min/max, bubbling that up in the recursion. At each step, check if you have a maxDiff using the current node, min and max. And you accomplish O(N)-time. Cheers, ACC.
public class Solution
{
public int MaxAncestorDiff(TreeNode root)
{
int maxDiff = -1;
int min = -1;
int max = 100001;
MaxAncestorDiff(root, ref maxDiff, ref min, ref max);
return maxDiff;
}
private void MaxAncestorDiff(TreeNode node,
ref int maxDiff,
ref int min,
ref int max)
{
if (node == null) return;
int minLeft = 100001;
int maxLeft = -1;
MaxAncestorDiff(node.left, ref maxDiff, ref minLeft, ref maxLeft);
int minRight = 100001;
int maxRight = -1;
MaxAncestorDiff(node.right, ref maxDiff, ref minRight, ref maxRight);
min = Math.Min(minLeft, minRight);
max = Math.Max(maxLeft, maxRight);
maxDiff = Math.Max(maxDiff, Math.Max(node.val - min, max - node.val));
min = Math.Min(min, node.val);
max = Math.Max(max, node.val);
}
}
1026. Maximum Difference Between Node and Ancestor
Medium
Given the
root of a binary tree, find the maximum value V for which there exists different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.
(A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.)
Example 1:

Input: [8,3,10,1,6,null,14,null,null,4,7,13] Output: 7 Explanation: We have various ancestor-node differences, some of which are given below : |8 - 3| = 5 |3 - 7| = 4 |8 - 1| = 7 |10 - 13| = 3 Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
Note:
- The number of nodes in the tree is between
2and5000. - Each node will have value between
0and100000.
If you think about the problem carefully, you'll realize that inevitably your answer will be of the form |A-B| where either A is the largest value in your tree, or B is the smallest. To prove this lemma, suppose that your solution is |A-B| and suppose that you have found another node C such that C<B. Well, |A-C| will be clearly be larger than |A-B|, hence |A-B| cannot be your solution.
That being said, you can do a post-order DFS keeping track of the min/max, bubbling that up in the recursion. At each step, check if you have a maxDiff using the current node, min and max. And you accomplish O(N)-time. Cheers, ACC.
public class Solution
{
public int MaxAncestorDiff(TreeNode root)
{
int maxDiff = -1;
int min = -1;
int max = 100001;
MaxAncestorDiff(root, ref maxDiff, ref min, ref max);
return maxDiff;
}
private void MaxAncestorDiff(TreeNode node,
ref int maxDiff,
ref int min,
ref int max)
{
if (node == null) return;
int minLeft = 100001;
int maxLeft = -1;
MaxAncestorDiff(node.left, ref maxDiff, ref minLeft, ref maxLeft);
int minRight = 100001;
int maxRight = -1;
MaxAncestorDiff(node.right, ref maxDiff, ref minRight, ref maxRight);
min = Math.Min(minLeft, minRight);
max = Math.Max(maxLeft, maxRight);
maxDiff = Math.Max(maxDiff, Math.Max(node.val - min, max - node.val));
min = Math.Min(min, node.val);
max = Math.Max(max, node.val);
}
}




Comments
Post a Comment