Validate Binary Tree Nodes

Problem is here: https://leetcode.com/problems/validate-binary-tree-nodes/

1361. Validate Binary Tree Nodes

Medium

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

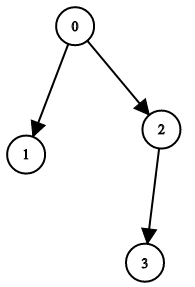
Example 1:

Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

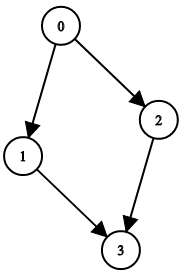
Example 2:

Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

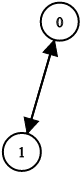
Example 3:

Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

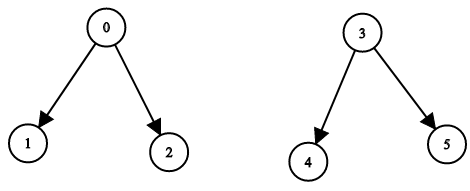
Example 4:

Input: n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1]
Output: false

Constraints:

• 1 <= n <= 10^4
• leftChild.length == rightChild.length == n
• -1 <= leftChild[i], rightChild[i] <= n - 1

Approach:
1. Detect whether there is only one potential root. This can be done in O(n). If there isn't, return false
2. Given (1), do a DFS ensuring that we can cover all nodes only once. This can be done in O(n).

Code is below, cheers, ACC.

public class Solution
{
    public bool ValidateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild)
    {
        //Check whether there is a single root
        int[] rootCandidates = new int[n];

        for (int i = 0; i < leftChild.Length; i++)
        {
            if (leftChild[i] >= 0 && leftChild[i] < n)
            {
                rootCandidates[leftChild[i]] = 1;
            }
            if (rightChild[i] >= 0 && rightChild[i] < n)
            {
                rootCandidates[rightChild[i]] = 1;
            }
        }

        int potentialRoot = -1;
        for (int i = 0; i < n; i++)
        {
            if (rootCandidates[i] == 0)
            {
                if (potentialRoot != -1) return false;
                potentialRoot = i;
            }
        }
        if (potentialRoot == -1) return false;

        //Check
        Hashtable visited = new Hashtable();
        if (!CheckBinaryTree(potentialRoot, leftChild, rightChild, visited)) return false;

        if (visited.Count != n) return false;

        return true;
    }

    private bool CheckBinaryTree(int nodeIndex,
                                    int[] leftChild,
                                    int[] rightChild,
                                    Hashtable visited)
    {
        if (nodeIndex == -1) return true;

        if (visited.ContainsKey(nodeIndex)) return false;
        visited.Add(nodeIndex, true);

        return CheckBinaryTree(leftChild[nodeIndex], leftChild, rightChild, visited) && CheckBinaryTree(rightChild[nodeIndex], leftChild, rightChild, visited);
    }
}