Maximum Product of Splitted Binary Tree

-
Three simple concepts in this problem, here is the problem: https://leetcode.com/problems/maximum-product-of-splitted-binary-tree/

1343. Maximum Product of Splitted Binary Tree
Medium
Given a binary tree root. Split the binary tree into two subtrees by removing 1 edge such that the product of the sums of the subtrees are maximized.
Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:
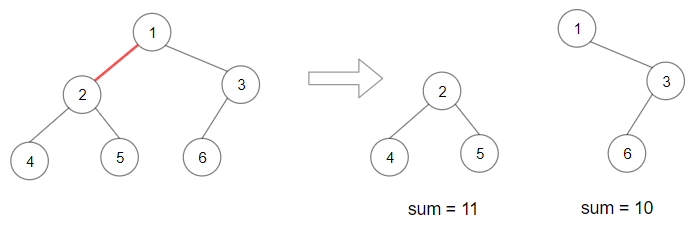
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)
Example 2:
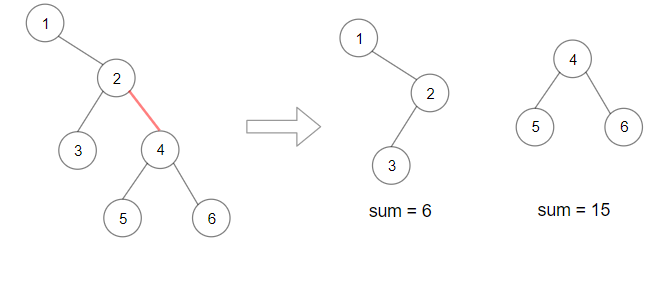
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation:  Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)
Example 3:
Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025
Example 4:
Input: root = [1,1]
Output: 1

Constraints:
  • Each tree has at most 50000 nodes and at least 2 nodes.
  • Each node's value is between [1, 10000].
It can be solved in O(n)-time and O(1)-space, using the following concepts:

  1. Utilization of Post-Order Traversal (SetValSumNodes)
  2. Reusing the node val to store the sum of all the elements for that sub-tree
  3. BigInteger computation (Numerics library) followed by the mod 10^9 + 7
Notice that due to #2, you can compute the current product in constant time (current product: (root.val - currentNode.left.val) * currentNode.left.val). Code is below, cheers, ACC.


public class Solution
{
    public int MaxProduct(TreeNode root)
    {
        if (root == null) return 0;

        BigInteger val = -1;
        SetValSumNodes(root);
        MaxProduct(root, root.val, ref val);
        return (int)(val % 1000000007);
    }

    private void MaxProduct(TreeNode node,
                            int sumAllNodes,
                            ref BigInteger prod)
    {
        if (node == null || (node.left == null && node.right == null)) return;
        if (node.left != null)
        {
            BigInteger current = (BigInteger)(sumAllNodes - node.left.val) * node.left.val;
            prod = BigInteger.Max(prod, current);
        }
        if (node.right != null)
        {
            BigInteger current = (BigInteger)(sumAllNodes - node.right.val) * node.right.val;
            prod = BigInteger.Max(prod, current);
        }
        MaxProduct(node.left, sumAllNodes, ref prod);
        MaxProduct(node.right, sumAllNodes, ref prod);
    }

    private void SetValSumNodes(TreeNode node)
    {
        if (node == null) return;
        SetValSumNodes(node.left);
        SetValSumNodes(node.right);
        if (node.left != null) node.val += node.left.val;
        if (node.right != null) node.val += node.right.val;
    }
}

Comments

Post a Comment

Popular posts from this blog

Advent of Code - Day 6, 2024: BFS and FSM

-
Image
To solve this Advent of Code (parts 1 and 2), I used Breadth-First Search (BFS) to keep moving the guard as well as Finite State Machine (FSM) to control the directions. This solves part 1 easily. Part 2 can be solved using the same technique, takes a little longer since you need to try every empty cell, but it eventually does the trick (takes a min or so). Code is down below, cheers, ACC. Day 6 - Advent of Code 2024 using System.IO; using System.Collections; using System; using System.Text; using System.Text.RegularExpressions; using System.ComponentModel.DataAnnotations; Process2(); void Process() { string fileName = "input.txt"; FileInfo fileInfo = new FileInfo(fileName); StreamReader sr = fileInfo.OpenText(); List map = new List (); int startRow = 0; int startCol = 0; while (!sr.EndOfStream) { string line = sr.ReadLine().Trim(); map.Add(new StringBuilder(line)); int indexStart = line.IndexOf('^'); ...
Read more

Golang vs. C#: performance characteristics (simple case study)

-
Image
This is an interesting example to study the performance characteristics of Golang compared to C# for a very particular case (not generalized though).  The same code was written in C# and Golang (literally translated from one to the other). Below you'll be able to see the source code for both. The problem is a simple post-order DFS in a tree-like graph. The code in C# times out (TLE = Time Limited Exceeded). The code in Golang not only works but beats 100% of the other Golang submissions. Take a look the image below: Some potential reasons for the performance gains from Go in this particular example are: 1. Language and Runtime Differences:    Go is compiled directly to machine code, while C# typically runs on a virtual machine (CLR).    Go has a simpler runtime with less overhead compared to the .NET runtime.    Go's garbage collector is designed for low latency, which can lead to better performance in some scenarios. 2. Data Structures:    G...
Read more

Advent of Code - Day 7, 2024: Backtracking and Eval

-
Image
Problem today requires backtracking and eval (evaluating a mathematical expression in the format of a string). Glad that it used a left-2-right evaluation, makes for an easy parsing and not overly complicated evaluation function. Code is down below for parts 1 and 2. Cheers, ACC. Day 7 - Advent of Code 2024 using System.IO; using System.Collections; using System; using System.Text; using System.Text.RegularExpressions; using System.ComponentModel.DataAnnotations; Process2(); void Process() { string fileName = "input.txt"; long retVal = 0; FileInfo fileInfo = new FileInfo(fileName); StreamReader sr = fileInfo.OpenText(); while (!sr.EndOfStream) { string line = sr.ReadLine().Trim(); string[] parts1 = line.Split(':'); long target = Int64.Parse(parts1[0]); string[] numbers = parts1[1].Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries); if (TryAll1(numbers, target, "", 0)) r...
Read more