Cinema Seat Allocation

Problem is here: https://leetcode.com/problems/cinema-seat-allocation/

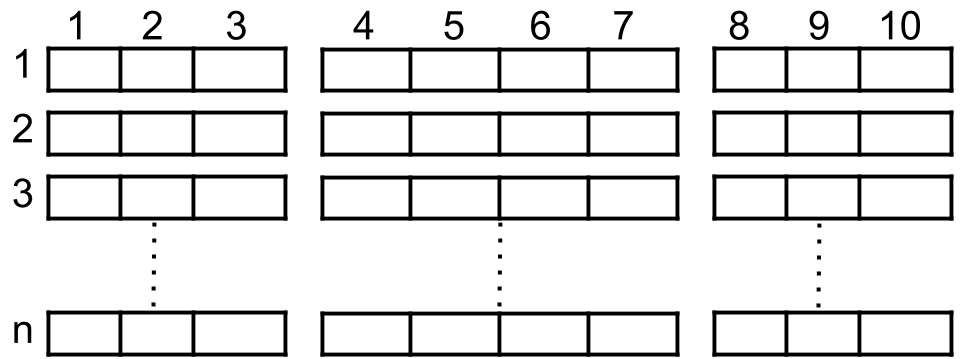
A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.

Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i]=[3,8] means the seat located in row 3 and labelled with 8 is already reserved. 

Return the maximum number of four-person families you can allocate on the cinema seats. A four-person family occupies fours seats in one row, that are next to each other. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be next to each other, however, It is permissible for the four-person family to be separated by an aisle, but in that case, exactly two people have to sit on each side of the aisle.

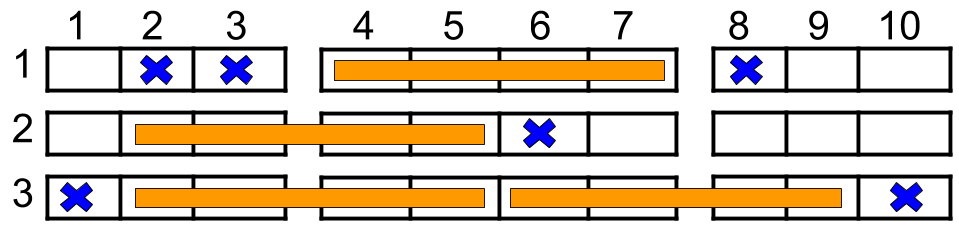
Example 1:

Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
Explanation: The figure above shows the optimal allocation for four families, where seats mark with blue are already reserved and contiguous seats mark with orange are for one family. 

Example 2:

Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2

Example 3:

Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
Output: 4

Constraints:

• 1 <= n <= 10^9
• 1 <= reservedSeats.length <= min(10*n, 10^4)
• reservedSeats[i].length == 2
• 1 <= reservedSeats[i][0] <= n
• 1 <= reservedSeats[i][1] <= 10
• All reservedSeats[i] are distinct.

You want to make sure you don't write an algorithm in O(n) since n = 10^9 (that's too long for O(n)). Rather, you will want to write the code in O(reservedSeats.length) which would be O(10^4). Strategy:

A) First, notice that the maximum possible for a row is 2 groups

B) Create a mapping between a seat and the starting position where you cannot start a new group. Here it is:

1: 0
2: 2
3: 2
4: 4, 2
5: 4, 2
6: 4, 6
7: 4, 6
8: 6
9: 6
10: 0

C) Go thru all the reserved seats and using B have a hash table per row flagging the positions that you cannot start a new group

D) Using boolean algebra you can figure out the max per row for all the reserved seat rows:

2 4 6
0 0 0 = 2
0 0 1 = 1
0 1 0 = 1
0 1 1 = 1
1 0 0 = 1
1 0 1 = 1
1 1 0 = 1
1 1 1 = 0

E) The above will give you the max for all the rows for which there is a reserved seats. For all others, use rule A

Code is below, cheers, ACC.

public class Solution
{
    public int MaxNumberOfFamilies(int n, int[][] reservedSeats)
    {
        Hashtable seatsStart = new Hashtable();

        for (int i = 0; i < reservedSeats.Length; i++)
        {
            int row = reservedSeats[i][0];
            int col = reservedSeats[i][1];

            if (!seatsStart.ContainsKey(row)) seatsStart.Add(row, new Hashtable());
            Hashtable seat = (Hashtable)seatsStart[row];

            if (col == 2 || col == 3)
            {
                if (!seat.ContainsKey(2)) seat.Add(2, true);
            }
            else if (col == 4 || col == 5)
            {
                if (!seat.ContainsKey(4)) seat.Add(4, true);
                if (!seat.ContainsKey(2)) seat.Add(2, true);
            }
            else if (col == 6 || col == 7)
            {
                if (!seat.ContainsKey(4)) seat.Add(4, true);
                if (!seat.ContainsKey(6)) seat.Add(6, true);
            }
            else if (col == 8 || col == 9)
            {
                if (!seat.ContainsKey(6)) seat.Add(6, true);
            }
        }

        int total = (n - seatsStart.Count) * 2;
        foreach (int key in seatsStart.Keys)
        {
            Hashtable seat = (Hashtable)seatsStart[key];
            if (seat.Count == 0) total += 2;
            else if (seat.Count < 3) total++;
        }

        return total;
    }
}