Graph Bipartition: coloring using BFS

This turned out to be a more complicated implementation than I thought, and I think a simple DFS would have been a better choice, but I decided to go with a BFS pushing each node to its own group. Lots of failures and little hacks along the way to make it work, finally it did.

Btw, go watch Spider Man No Way Home, top 5 Marvel Movies ever!!!

Code is below, cheers, ACC.

Is Graph Bipartite? - LeetCode

785. Is Graph Bipartite?

Medium

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

• There are no self-edges (graph[u] does not contain u).
• There are no parallel edges (graph[u] does not contain duplicate values).
• If v is in graph[u], then u is in graph[v] (the graph is undirected).
• The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

 

Example 1:

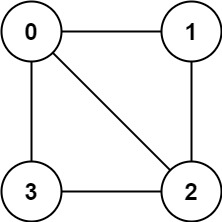
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

 

Constraints:

• graph.length == n
• 1 <= n <= 100
• 0 <= graph[u].length < n
• 0 <= graph[u][i] <= n - 1
• graph[u] does not contain u.
• All the values of graph[u] are unique.
• If graph[u] contains v, then graph[v] contains u.

Accepted

248,435

Submissions

499,316

public bool IsBipartite(int[][] graph)
{
    Hashtable htGraph = new Hashtable();
    int n = 0;
    int totalNumberEdges = 0;
    for (int i = 0; i < graph.Length; i++)
    {
        for (int j = 0; j < graph[i].Length; j++)
        {
            int[] nodesFrom = { i, graph[i][j] };
            int[] nodesTo = { graph[i][j], i };

            for (int z = 0; z < nodesFrom.Length; z++)
            {
                if (!htGraph.ContainsKey(nodesFrom[z])) htGraph.Add(nodesFrom[z], new Hashtable());
                Hashtable connections = (Hashtable)htGraph[nodesFrom[z]];
                if (!connections.ContainsKey(nodesTo[z]))
                {
                    connections.Add(nodesTo[z], true);
                    totalNumberEdges++;
                }
            }
            n = Math.Max(n, graph[i][j]);
        }
    }
    n++;
    totalNumberEdges /= 2;

    Hashtable group0 = new Hashtable();
    Hashtable group1 = new Hashtable();
    Hashtable usedEdges = new Hashtable();
    for (int i = 0; i < n; i++)
    {
        if (!group0.ContainsKey(i) && 
            !group1.ContainsKey(i) && 
            IsBipartite(i, n, htGraph, group0, group1, totalNumberEdges, usedEdges)) return true;
    }
    return false;
}

public class BipartiteQueueItem
{
    public int nodeFrom = 0;
    public int nodeTo = 0;
    public int group = 0;
    public int key = 0;

    public BipartiteQueueItem(int nodeFrom, int nodeTo, int group)
    {
        this.nodeFrom = nodeFrom;
        this.nodeTo = nodeTo;
        this.group = group;
        this.key = Math.Min(nodeFrom, nodeTo) * 10007 + Math.Max(nodeFrom, nodeTo);
    }
}

public bool IsBipartite(int node,
                        int n,
                        Hashtable graph,
                        Hashtable group0,
                        Hashtable group1,
                        int totalNumberEdges,
                        Hashtable usedEdges)
{
    Queue queue = new Queue();
    BipartiteQueueItem queueItem = new BipartiteQueueItem(-1, node, 0);
    queue.Enqueue(queueItem);
    group0.Add(queueItem.nodeTo, true);

    while (queue.Count > 0)
    {
        BipartiteQueueItem currentQueueItem = queue.Dequeue();

        if (graph.ContainsKey(currentQueueItem.nodeTo))
        {
            Hashtable connections = (Hashtable)graph[currentQueueItem.nodeTo];
            foreach (int connection in connections.Keys)
            {
                if (connection != currentQueueItem.nodeFrom)
                {
                    BipartiteQueueItem newQueueItem = null;
                    if (currentQueueItem.group == 0)
                    {
                        if (group0.ContainsKey(connection)) return false;
                        newQueueItem = new BipartiteQueueItem(currentQueueItem.nodeTo, connection, (currentQueueItem.group + 1) % 2);
                        if (!group1.ContainsKey(connection))
                        {
                            group1.Add(connection, true);
                            queue.Enqueue(newQueueItem);
                        }
                        if (!usedEdges.ContainsKey(newQueueItem.key)) usedEdges.Add(newQueueItem.key, true);
                    }
                    else
                    {
                        if (group1.ContainsKey(connection)) return false;
                        newQueueItem = new BipartiteQueueItem(currentQueueItem.nodeTo, connection, (currentQueueItem.group + 1) % 2);
                        if (!group0.ContainsKey(connection))
                        {
                            group0.Add(connection, true);
                            queue.Enqueue(newQueueItem);
                        }
                        if (!usedEdges.ContainsKey(newQueueItem.key)) usedEdges.Add(newQueueItem.key, true);
                    }
                }
            }
        }
    }

    return usedEdges.Count == totalNumberEdges && (group0.Count + group1.Count == n);
}