Application of Floyd–Warshall Algorithm

Robert Floyd and Stephen Warshall (in the pictures below, from Wikipedia) died relatively young for today's standards. It was a pity as I believe they would have had at least another strong productive 20 years ahead of them. But they left us a great legacy, one of them int the Floyd–Warshall Algorithm.

This algorithm manages to calculate the distance between any two nodes (a,b) in a graph in O(n^3), which is unbelievably fast. Notice that it does beat Dijkstra since this one only allows you to find the min distance between a node and all the other ones, whereas Floyd-Warshall gives you a nice nxn table with all the distances. It is a variation of Dynamic Programming.

This problem below requires the use of Floyd–Warshall Algorithm. Once you have the table with the min distance across all the nodes (and remember since n=10^2, the algorithm will run in 10^6, very tractable), then a simple n^2 parse is required to find the solution. Code is down below, cheers, ACC.

Find the City With the Smallest Number of Neighbors at a Threshold Distance - LeetCode

1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance

Medium

There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distanceThreshold.

Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.

Notice that the distance of a path connecting cities i and j is equal to the sum of the edges' weights along that path.

 

Example 1:

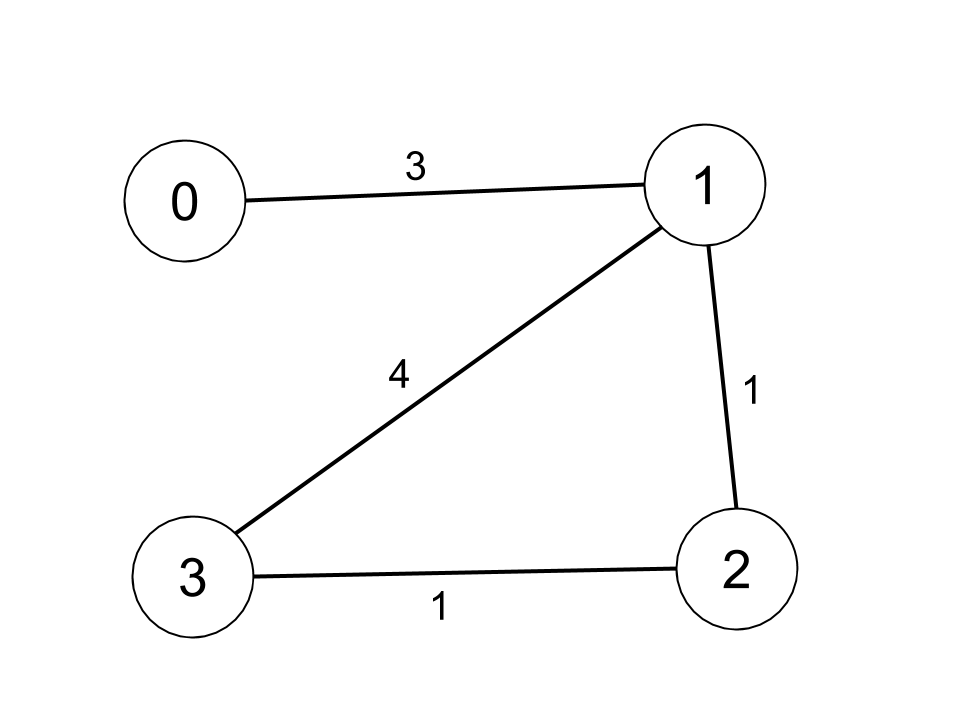
Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
Output: 3
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> [City 1, City 2] 
City 1 -> [City 0, City 2, City 3] 
City 2 -> [City 0, City 1, City 3] 
City 3 -> [City 1, City 2] 
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.

Example 2:

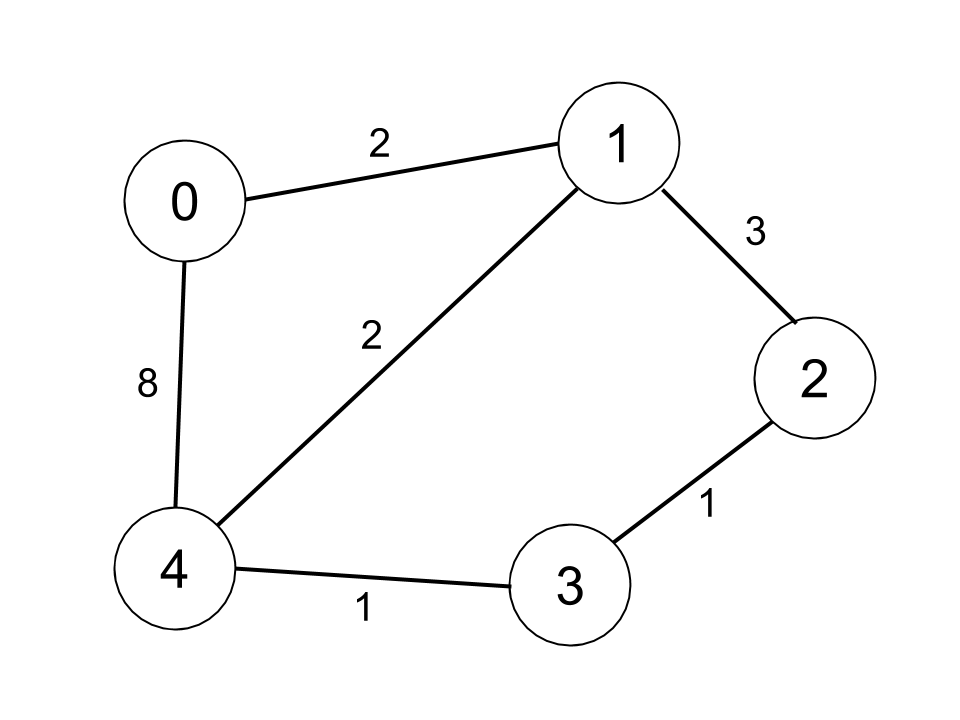
Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
Output: 0
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> [City 1] 
City 1 -> [City 0, City 4] 
City 2 -> [City 3, City 4] 
City 3 -> [City 2, City 4]
City 4 -> [City 1, City 2, City 3] 
The city 0 has 1 neighboring city at a distanceThreshold = 2.

 

Constraints:

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti, distanceThreshold <= 10^4
• All pairs (fromi, toi) are distinct.

Accepted

33,601

Submissions

66,743

public class Solution
{
    public int FindTheCity(int n, int[][] edges, int distanceThreshold)
    {
        //Build the graph
        Hashtable graph = new Hashtable();
        for (int i = 0; i < edges.Length; i++)
        {
            for (int j = 0; j < 2; j++)
            {
                if (!graph.ContainsKey(edges[i][j])) graph.Add(edges[i][j], new Hashtable());
                Hashtable connection = (Hashtable)graph[edges[i][j]];
                if (!connection.ContainsKey(edges[i][(j + 1) % 2])) connection.Add(edges[i][(j + 1) % 2], edges[i][2]);
            }
        }

        int[,] distance = null;

        FloydWarshall(n, graph, ref distance);
        int city = 0;
        int reachable = Int32.MaxValue;
        for (int i = 0; i < n; i++)
        {
            int count = 0;
            for (int j = 0; j < n; j++)
            {
                if (i != j && distance[i, j] <= distanceThreshold) count++;
            }
            if (count <= reachable)
            {
                reachable = count;
                city = i;
            }
        }

        return city;
    }

    public void FloydWarshall(int n, Hashtable graph, ref int[,] distance)
    {
        distance = new int[n, n];
        int INF = 1000000;

        for (int i = 0; i < n; i++)
        {
            Hashtable connection = null;

            if (graph.ContainsKey(i)) connection = (Hashtable)graph[i];
            for (int j = 0; j < n; j++)
            {
                if (connection == null || !connection.ContainsKey(j))
                {
                    distance[i, j] = INF;
                }
                else
                {
                    distance[i, j] = (int)connection[j];
                }
            }
        }

        for (int k = 0; k < n; k++)
        {
            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < n; j++)
                {
                    if (distance[i, k] + distance[k, j] < distance[i, j])
                        distance[i, j] = distance[i, k] + distance[k, j];
                }
            }
        }
    }
}