Min Spanning Tree

Problem involves searching for a min spanning tree in a graph. Basically the algorithm to find the min spanning tree can start from any node in the tree, and it runs in O(n) nodes using BFS. We then try it out by removing each edge at a time, from the back to the front. At the end it should take O(number of nodes * number of edges). Since both are ~10^3, we're talking about 1M interactions, which is relatively fast. Code is down below, cheers, ACC.

Redundant Connection - LeetCode

684. Redundant Connection

Medium

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

 

Example 1:

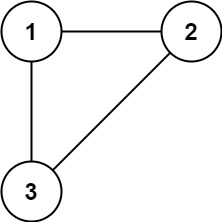
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

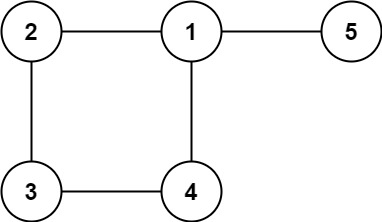
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

 

Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• There are no repeated edges.
• The given graph is connected.

Accepted

178,143

Submissions

293,431

public int[] FindRedundantConnection(int[][] edges)
{
    Hashtable graph = new Hashtable();
    int n = 0;
    for (int i = 0; i < edges.Length; i++)
    {
        for (int j = 0; j < 2; j++)
        {
            if (!graph.ContainsKey(edges[i][j])) graph.Add(edges[i][j], new Hashtable());
            Hashtable connections = (Hashtable)graph[edges[i][j]];
            if (!connections.ContainsKey(edges[i][(j + 1) % 2])) connections.Add(edges[i][(j + 1) % 2], true);

            n = Math.Max(n, edges[i][j]);
        }
    }

    int[] retVal = new int[2];
    for (int i = edges.Length - 1; i >= 0; i--)
    {
        if (MinSpanningTreeBFS(n, graph, edges[i][0], edges[i][1]))
        {
            retVal[0] = edges[i][0];
            retVal[1] = edges[i][1];
            break;
        }
    }

    return retVal;
}

public bool MinSpanningTreeBFS(int n,
                                Hashtable graph,
                                int removedEdgeFrom,
                                int removedEdgeTo)
{
    Queue queue = new Queue();
    SpanningTreeQueueItem queueItem = new SpanningTreeQueueItem(-1, 1);
    queue.Enqueue(queueItem);
    Hashtable visited = new Hashtable();
    visited.Add(queueItem.nodeTo, true);

    while (queue.Count > 0 && visited.Count < n)
    {
        SpanningTreeQueueItem currentQueueItem = queue.Dequeue();

        if (graph.ContainsKey(currentQueueItem.nodeTo))
        {
            Hashtable connections = (Hashtable)graph[currentQueueItem.nodeTo];
            foreach (int connection in connections.Keys)
            {
                if ((currentQueueItem.nodeTo == removedEdgeFrom && connection == removedEdgeTo) ||
                    (currentQueueItem.nodeTo == removedEdgeTo && connection == removedEdgeFrom)) continue;

                if (connection != currentQueueItem.nodeFrom)
                {
                    SpanningTreeQueueItem newQueueItem = new SpanningTreeQueueItem(currentQueueItem.nodeTo, connection);
                    if (visited.ContainsKey(newQueueItem.nodeTo))
                    {
                        return false;
                    }
                    else
                    {
                        visited.Add(newQueueItem.nodeTo, true);
                        queue.Enqueue(newQueueItem);
                    }
                }
            }
        }
    }

    return visited.Count == n;
}

public class SpanningTreeQueueItem
{
    public int nodeFrom;
    public int nodeTo;

    public SpanningTreeQueueItem(int nodeFrom, int nodeTo)
    {
        this.nodeFrom = nodeFrom;
        this.nodeTo = nodeTo;
    }
}