Saturday Night Dijkstra's Algorithm
Covid days (and nights) are still amongst us, especially now with the sucky Omicron Variant. Stuck at home, yet again, we resort to our dear friend Dijkstra:
In this latest problem on Leetcode (959th solved), we see another by-the-book invitation to solve a problem using Dijkstra's Algorithm. There is a graph, with weights, and you want to minimize the cost (I'm sure there is a DP algorithm for that too, but I'm not that good in DP as I mentioned many times before). The problem adds a "tweak" since now you have a max of N discounts that you can apply. This really doesn't change the problem that much: in each interaction, you should assume (a) adding a new connection with the discount (if allowed) and (b) adding a new connection without. So max of two potential enqueue calls for each connection.
Recapping what Dijkstra's is:
1/ It is a BFS algorithm
2/ But it uses a Priority Queue, rather than just a Queue
3/ You only mark as "visited" during the dequeue - never during the enqueue
4/ You allow the same connected node to be enqueued multiple times (different weights), that's why you never mark as visited during the enqueue
5/ Time complexity is of the order O((V+E)LogV), where V is the number of vertices and E the number of edges. In our case, V = E = 1000, hence O(2000*Log(1000)), very fast.
Problem and code are below, cheers, and stay safe! ACC.
Minimum Cost to Reach City With Discounts - LeetCode
A series of highways connect n cities numbered from 0 to n - 1. You are given a 2D integer array highways where highways[i] = [city1i, city2i, tolli] indicates that there is a highway that connects city1i and city2i, allowing a car to go from city1i to city2i and vice versa for a cost of tolli.
You are also given an integer discounts which represents the number of discounts you have. You can use a discount to travel across the ith highway for a cost of tolli / 2 (integer division). Each discount may only be used once, and you can only use at most one discount per highway.
Return the minimum total cost to go from city 0 to city n - 1, or -1 if it is not possible to go from city 0 to city n - 1.
Example 1: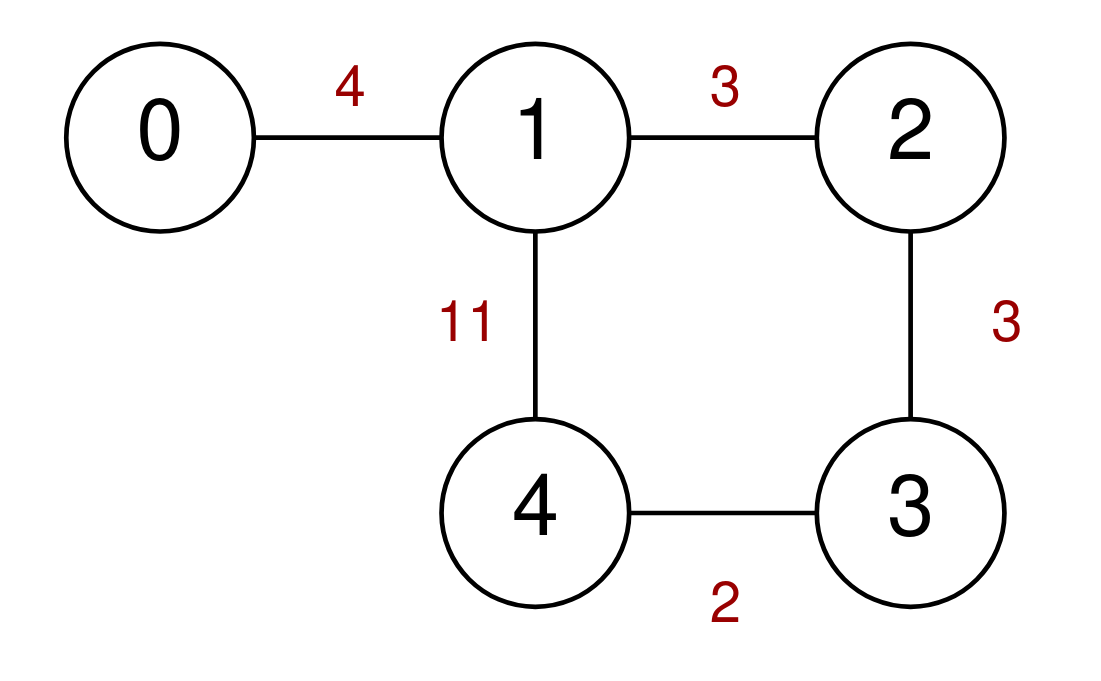
Input: n = 5, highways = [[0,1,4],[2,1,3],[1,4,11],[3,2,3],[3,4,2]], discounts = 1 Output: 9 Explanation: Go from 0 to 1 for a cost of 4. Go from 1 to 4 and use a discount for a cost of 11 / 2 = 5. The minimum cost to go from 0 to 4 is 4 + 5 = 9.
Example 2: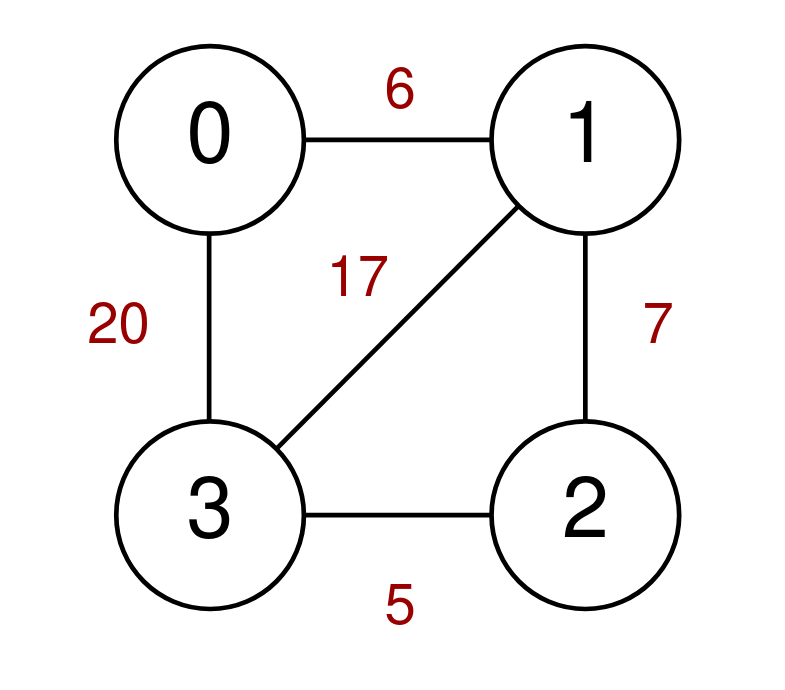
Input: n = 4, highways = [[1,3,17],[1,2,7],[3,2,5],[0,1,6],[3,0,20]], discounts = 20 Output: 8 Explanation: Go from 0 to 1 and use a discount for a cost of 6 / 2 = 3. Go from 1 to 2 and use a discount for a cost of 7 / 2 = 3. Go from 2 to 3 and use a discount for a cost of 5 / 2 = 2. The minimum cost to go from 0 to 3 is 3 + 3 + 2 = 8.
Example 3: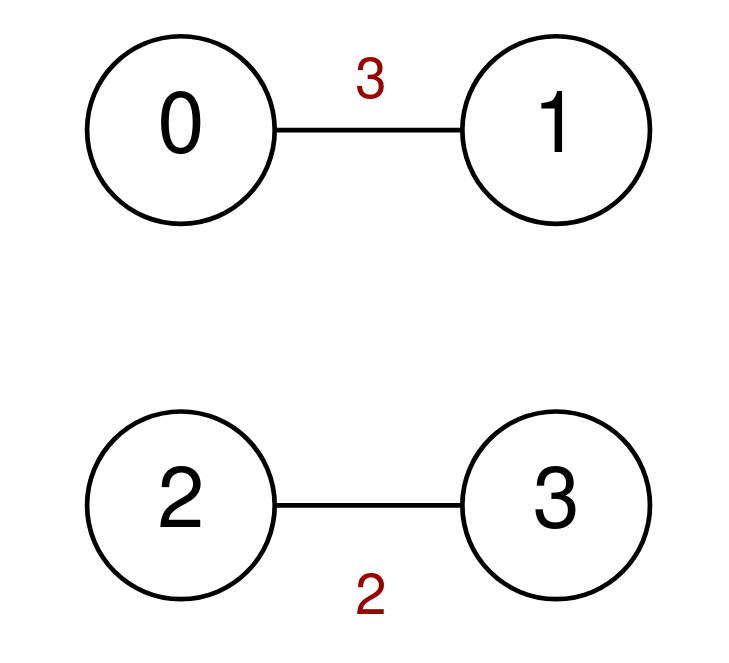
Input: n = 4, highways = [[0,1,3],[2,3,2]], discounts = 0 Output: -1 Explanation: It is impossible to go from 0 to 3 so return -1.
Constraints:
2 <= n <= 10001 <= highways.length <= 1000highways[i].length == 30 <= city1i, city2i <= n - 1city1i != city2i0 <= tolli <= 1050 <= discounts <= 500- There are no duplicate highways.
public class Solution
{
public class PriorityQueue
{
public struct HeapEntry
{
private object item;
private double priority;
public HeapEntry(object item, double priority)
{
this.item = item;
this.priority = priority;
}
public object Item
{
get
{
return item;
}
}
public double Priority
{
get
{
return priority;
}
}
}
private bool ascend;
private int count;
private int capacity;
private HeapEntry[] heap;
public int Count
{
get
{
return this.count;
}
}
public PriorityQueue(bool ascend)
{
capacity = 1000000;
heap = new HeapEntry[capacity];
this.ascend = ascend;
}
public object Dequeue(out double priority)
{
priority = heap[0].Priority;
object result = heap[0].Item;
count--;
trickleDown(0, heap[count]);
return result;
}
public object Peak(/*out double priority*/)
{
//priority = heap[0].Priority;
object result = heap[0].Item;
return result;
}
public void Enqueue(object item, double priority)
{
count++;
bubbleUp(count - 1, new HeapEntry(item, priority));
}
private void bubbleUp(int index, HeapEntry he)
{
int parent = (index - 1) / 2;
// note: (index > 0) means there is a parent
if (this.ascend)
{
while ((index > 0) && (heap[parent].Priority > he.Priority))
{
heap[index] = heap[parent];
index = parent;
parent = (index - 1) / 2;
}
heap[index] = he;
}
else
{
while ((index > 0) && (heap[parent].Priority < he.Priority))
{
heap[index] = heap[parent];
index = parent;
parent = (index - 1) / 2;
}
heap[index] = he;
}
}
private void trickleDown(int index, HeapEntry he)
{
int child = (index * 2) + 1;
while (child < count)
{
if (this.ascend)
{
if (((child + 1) < count) &&
(heap[child].Priority > heap[child + 1].Priority))
{
child++;
}
}
else
{
if (((child + 1) < count) &&
(heap[child].Priority < heap[child + 1].Priority))
{
child++;
}
}
heap[index] = heap[child];
index = child;
child = (index * 2) + 1;
}
bubbleUp(index, he);
}
}
public class MCQueueItem
{
public int city = 0;
public int totalCost = 0;
public int discountsLeft = 0;
public MCQueueItem(int city, int totalCost, int discountsLeft)
{
this.city = city;
this.totalCost = totalCost;
this.discountsLeft = discountsLeft;
}
}
public int MinimumCost(int n, int[][] highways, int discounts)
{
Hashtable graph = new Hashtable();
for (int i = 0; i < highways.Length; i++)
{
int[] cities = { highways[i][0], highways[i][1] };
for (int j = 0; j < cities.Length; j++)
{
if (!graph.ContainsKey(cities[j])) graph.Add(cities[j], new Hashtable());
Hashtable connections = (Hashtable)graph[cities[j]];
if (!connections.ContainsKey(cities[(j + 1) % 2])) connections.Add(cities[(j + 1) % 2], highways[i][2]);
}
}
int startCity = 0;
int finishCity = n - 1;
PriorityQueue pQueue = new PriorityQueue(true);
Hashtable visited = new Hashtable();
MCQueueItem queueItem = new MCQueueItem(startCity, 0, discounts);
pQueue.Enqueue(queueItem, queueItem.totalCost);
while (pQueue.Count > 0)
{
double tempTotalCost = 0;
MCQueueItem currentCity = (MCQueueItem)pQueue.Dequeue(out tempTotalCost);
//When using Djkistra, only mark during the dequeue, not during the enqueue
if (!visited.ContainsKey(currentCity.city)) visited.Add(currentCity.city, true);
if (currentCity.city == finishCity)
{
return currentCity.totalCost;
}
if (graph.ContainsKey(currentCity.city))
{
Hashtable connections = (Hashtable)graph[currentCity.city];
foreach (int connectedCity in connections.Keys)
{
if (!visited.ContainsKey(connectedCity))
{
//Two cases to add:
//1. applying the discount
if (currentCity.discountsLeft > 0)
{
MCQueueItem queueItem1 = new MCQueueItem(connectedCity, currentCity.totalCost + ((int)connections[connectedCity]) / 2, currentCity.discountsLeft - 1);
pQueue.Enqueue(queueItem1, queueItem1.totalCost);
}
//2. not applying the discount
MCQueueItem queueItem2 = new MCQueueItem(connectedCity, currentCity.totalCost + (int)connections[connectedCity], currentCity.discountsLeft);
pQueue.Enqueue(queueItem2, queueItem2.totalCost);
}
}
}
}
return -1;
}
}





Comments
Post a Comment