LC Hard Problem: Follow the Hints

Shamelessly looked at the hints for this LC hard problem. The hints here actually describe the algorithm step-by-step; it describes the three functions you need to implement (I implemented a fourth one to handle short products). Learned few interesting math concepts by solving this problem, such as how to calculate trailing zeroes quickly and the first five digits of a number using logarithms. Code is down below, cheers, ACC

Abbreviating the Product of a Range - LeetCode

2117. Abbreviating the Product of a Range

Hard

You are given two positive integers left and right with left <= right. Calculate the product of all integers in the inclusive range [left, right].

Since the product may be very large, you will abbreviate it following these steps:

1. Count all trailing zeros in the product and remove them. Let us denote this count as C.
   • For example, there are 3 trailing zeros in 1000, and there are 0 trailing zeros in 546.
2. Denote the remaining number of digits in the product as d. If d > 10, then express the product as <pre>...<suf> where <pre> denotes the first 5 digits of the product, and <suf> denotes the last 5 digits of the product after removing all trailing zeros. If d <= 10, we keep it unchanged.
   • For example, we express 1234567654321 as 12345...54321, but 1234567 is represented as 1234567.
3. Finally, represent the product as a string "<pre>...<suf>eC".
   • For example, 12345678987600000 will be represented as "12345...89876e5".

Return a string denoting the abbreviated product of all integers in the inclusive range [left, right].

 

Example 1:

Input: left = 1, right = 4
Output: "24e0"
Explanation:
The product is 1 × 2 × 3 × 4 = 24.
There are no trailing zeros, so 24 remains the same. The abbreviation will end with "e0".
Since the number of digits is 2, which is less than 10, we do not have to abbreviate it further.
Thus, the final representation is "24e0". 

Example 2:

Input: left = 2, right = 11
Output: "399168e2"
Explanation:
The product is 39916800.
There are 2 trailing zeros, which we remove to get 399168. The abbreviation will end with "e2".
The number of digits after removing the trailing zeros is 6, so we do not abbreviate it further.
Hence, the abbreviated product is "399168e2".  

Example 3:

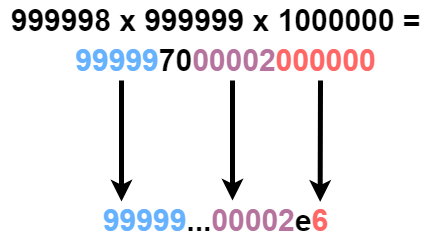
Input: left = 999998, right = 1000000
Output: "99999...00002e6"
Explanation:
The above diagram shows how we abbreviate the product to "99999...00002e6".
- It has 6 trailing zeros. The abbreviation will end with "e6".
- The first 5 digits are 99999.
- The last 5 digits after removing trailing zeros is 00002.

 

Constraints:

• 1 <= left <= right <= 106

Accepted

807

Submissions

3,352

public string AbbreviateProduct(int left, int right)
{
    string shortProduct = ShortProduct(left, right);

    if (!String.IsNullOrEmpty(shortProduct)) return shortProduct;

    int c = CountNumberTrailingZeroes(left, right);
    string last5 = CountLastFiveDigits(left, right, c);
    string first5 = CountFirstFiveDigits(left, right);

    return first5 + "..." + last5 + "e" + c.ToString();
}

public string ShortProduct(int left,
                            int right)
{
    BigInteger n = 1;
    int countTrailingZeroes = 0;
    for (int i = left; i <= right; i++)
    {
        n *= i;
        while (n % 10 == 0)
        {
            n /= 10;
            countTrailingZeroes++;
        }
        if (n.ToString().Length > 10) return "";
    }

    return n.ToString() + "e" + countTrailingZeroes.ToString();
}

private int CountNumberTrailingZeroes(int left, int right)
{
    int count2 = 0;
    int count5 = 0;

    for (int i = left; i <= right; i++)
    {
        int temp2 = i;
        while (temp2 % 2 == 0)
        {
            temp2 /= 2;
            count2++;
        }

        int temp5 = i;
        while (temp5 % 5 == 0)
        {
            temp5 /= 5;
            count5++;
        }
    }

    return Math.Min(count2, count5);
}

private string CountFirstFiveDigits(int left, int right)
{
    double sumLogs = 0;

    for (int i = left; i <= right; i++) sumLogs += Math.Log10(i);

    double y = sumLogs - (long)sumLogs;
    string retVal = Math.Floor(Math.Pow(10, y + 4)).ToString();

    if (retVal.Length > 5) retVal = retVal.Substring(0, 5);

    return retVal;
}

private string CountLastFiveDigits(int left, int right, int c)
{
    long product = 1;
    bool largeNumber = false;

    int min2 = c;
    int min5 = c;
    for (int i = left; i <= right; i++)
    {
        int t1 = i;
        while (t1 % 2 == 0 && min2 > 0)
        {
            t1 /= 2;
            min2--;
        }

        int t3 = t1;
        while (t3 % 5 == 0 && min5 > 0)
        {
            t3 /= 5;
            min5--;
        }

        if (product * t3 >= 100000) largeNumber = true;
        product = (product * t3) % (100000);
    }

    string result = product.ToString();

    if(largeNumber)
    {
        while (result.Length < 5) result = "0" + result;
    }

    return result;
}