Follow the hints!

Since the goal of LC is to learn, there is nothing wrong in following the hints whenever you get stuck. I got stuck in the problem below and took a look at the hints: pick any node, find the farthest node A from it, now find the farthest node B from A, and you have your answer. Clever, but I couldn't figure that out on my own. Still was left to implement the code. Down below, cheers, ACC.

Tree Diameter - LeetCode

1245. Tree Diameter

Medium

The diameter of a tree is the number of edges in the longest path in that tree.

There is an undirected tree of n nodes labeled from 0 to n - 1. You are given a 2D array edges where edges.length == n - 1 and edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the tree.

Return the diameter of the tree.

 

Example 1:

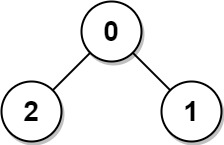
Input: edges = [[0,1],[0,2]]
Output: 2
Explanation: The longest path of the tree is the path 1 - 0 - 2.

Example 2:

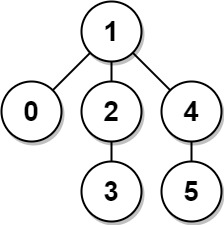
Input: edges = [[0,1],[1,2],[2,3],[1,4],[4,5]]
Output: 4
Explanation: The longest path of the tree is the path 3 - 2 - 1 - 4 - 5.

 

Constraints:

• n == edges.length + 1
• 1 <= n <= 104
• 0 <= ai, bi < n
• ai != bi

Accepted

27,125

Submissions

43,851

public int TreeDiameter(int[][] edges)
{
    Hashtable graph = new Hashtable();

    for (int i = 0; i < edges.Length; i++)
    {
        int a = edges[i][0];
        int b = edges[i][1];

        if (!graph.ContainsKey(a)) graph.Add(a, new Hashtable());
        Hashtable childrenA = (Hashtable)graph[a];
        if (!childrenA.ContainsKey(b)) childrenA.Add(b, true);

        if (!graph.ContainsKey(b)) graph.Add(b, new Hashtable());
        Hashtable childrenB = (Hashtable)graph[b];
        if (!childrenB.ContainsKey(a)) childrenB.Add(a, true);
    }

    //Step 1: from any node, find farthest
    int maxDistance = 0;
    int farthestNode = 0;
    Hashtable visited = new Hashtable();
    visited.Add(0, true);
    FindFarthestNode(0, graph, visited, 0, ref maxDistance, ref farthestNode);

    //Step 2: from farthestNode, find the path
    int newFarthestNode = 0;
    int diameter = 0;
    visited = new Hashtable();
    visited.Add(farthestNode, true);
    FindFarthestNode(farthestNode, graph, visited, 0, ref diameter, ref newFarthestNode);

    return diameter;
}

private void FindFarthestNode(int from,
                                Hashtable graph,
                                Hashtable visited,
                                int distance,
                                ref int maxDistance,
                                ref int farthestNode)
{
    if (distance > maxDistance)
    {
        maxDistance = distance;
        farthestNode = from;
    }

    if (graph.ContainsKey(from))
    {
        Hashtable children = (Hashtable)graph[from];
        foreach (int child in children.Keys)
        {
            if (!visited.ContainsKey(child))
            {
                visited.Add(child, true);
                FindFarthestNode(child, graph, visited, distance + 1, ref maxDistance, ref farthestNode);
            }
        }
    }
}