Map-Reduce Instance

I find the strategy to solving this problem an instance of the famous programming pattern "Map-Reduce", where you use step one to map a sparse subset of potential solutions to your problem, followed by a reduction of that subset into the actual solution.

The map in this case calculates the distance from a node to all the other nodes using a queue and BFS. The reduce simply goes to the two calculated distance arrays and retrieves the solution in linear time. Code is down below, cheers, ACC.

Find Closest Node to Given Two Nodes - LeetCode

2359. Find Closest Node to Given Two Nodes

Medium

You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from i, then edges[i] == -1.

You are also given two integers node1 and node2.

Return the index of the node that can be reached from both node1 and node2, such that the maximum between the distance from node1 to that node, and from node2 to that node is minimized. If there are multiple answers, return the node with the smallest index, and if no possible answer exists, return -1.

Note that edges may contain cycles.

 

Example 1:

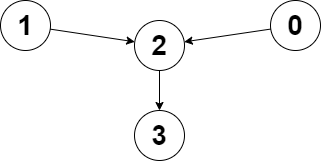
Input: edges = [2,2,3,-1], node1 = 0, node2 = 1
Output: 2
Explanation: The distance from node 0 to node 2 is 1, and the distance from node 1 to node 2 is 1.
The maximum of those two distances is 1. It can be proven that we cannot get a node with a smaller maximum distance than 1, so we return node 2.

Example 2:

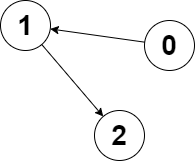
Input: edges = [1,2,-1], node1 = 0, node2 = 2
Output: 2
Explanation: The distance from node 0 to node 2 is 2, and the distance from node 2 to itself is 0.
The maximum of those two distances is 2. It can be proven that we cannot get a node with a smaller maximum distance than 2, so we return node 2.

 

Constraints:

• n == edges.length
• 2 <= n <= 105
• -1 <= edges[i] < n
• edges[i] != i
• 0 <= node1, node2 < n

Accepted

8,171

Submissions

28,468

public class ClosestNodeQueue
{
    public int node;
    public int steps;

    public ClosestNodeQueue(int node, int steps)
    {
        this.node = node;
        this.steps = steps;
    }
}
public int ClosestMeetingNode(int[] edges, int node1, int node2)
{
    int[] distance1 = new int[edges.Length];
    MapDistance(edges, node1, ref distance1);
    int[] distance2 = new int[edges.Length];
    MapDistance(edges, node2, ref distance2);

    int min = Int32.MaxValue;
    int retVal = -1;

    for (int i = 0; i < distance1.Length; i++)
    {
        if (distance1[i] != -1 && distance2[i] != -1 && Math.Max(distance1[i], distance2[i]) < min)
        {
            min = Math.Max(distance1[i], distance2[i]);
            retVal = i;
        }
    }

    return retVal;
}

public void MapDistance(int[] edges,
                        int node,
                        ref int[] distance)
{
    for (int i = 0; i < distance.Length; i++) distance[i] = -1;

    Queue queue = new Queue();
    Hashtable visited = new Hashtable();
    queue.Enqueue(new ClosestNodeQueue(node, 0));
    visited.Add(node, true);

    while (queue.Count > 0)
    {
        ClosestNodeQueue closestNode = queue.Dequeue();

        if (distance[closestNode.node] == -1) distance[closestNode.node] = closestNode.steps;

        if (edges[closestNode.node] != -1 && !visited.ContainsKey(edges[closestNode.node]))
        {
            visited.Add(edges[closestNode.node], true);
            queue.Enqueue(new ClosestNodeQueue(edges[closestNode.node], closestNode.steps + 1));
        }
    }
}