Grid in N^3

This actually is a simpler problem then it looks. Given the limit for N is O(10^2), an N^3 solution brings us to O(10^6), which is very tractable. Three nested loops (and a hash table) would do it. Code is down below, cheers, ACC.

Equal Row and Column Pairs - LeetCode

2352. Equal Row and Column Pairs

Medium

Given a 0-indexed n x n integer matrix grid, return the number of pairs (Ri, Cj) such that row Ri and column Cj are equal.

A row and column pair is considered equal if they contain the same elements in the same order (i.e. an equal array).

 

Example 1:

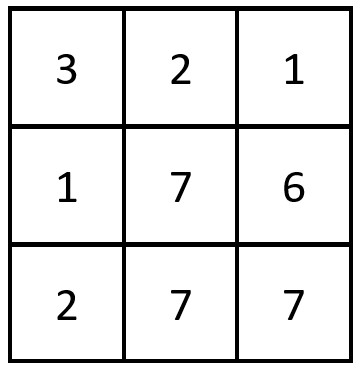
Input: grid = [[3,2,1],[1,7,6],[2,7,7]]
Output: 1
Explanation: There is 1 equal row and column pair:
- (Row 2, Column 1): [2,7,7]

Example 2:

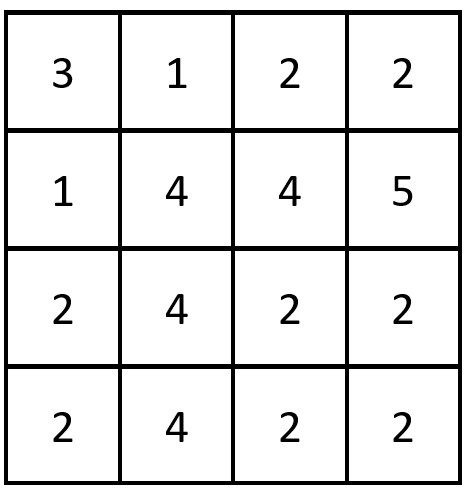
Input: grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
Output: 3
Explanation: There are 3 equal row and column pairs:
- (Row 0, Column 0): [3,1,2,2]
- (Row 2, Column 2): [2,4,2,2]
- (Row 3, Column 2): [2,4,2,2]

 

Constraints:

• n == grid.length == grid[i].length
• 1 <= n <= 200
• 1 <= grid[i][j] <= 105

public int EqualPairs(int[][] grid)
{
    int retVal = 0;

    for (int r = 0; r < grid.Length; r++)
    {
        Hashtable colBlockListed = new Hashtable();
        for (int c = 0; c < grid[r].Length; c++)
        {
            for (int c1 = 0; c1 < grid[r].Length; c1++)
            {
                if (grid[r][c] != grid[c][c1])
                {
                    if (!colBlockListed.ContainsKey(c1)) colBlockListed.Add(c1, true);
                }
            }
        }

        retVal += (grid[r].Length - colBlockListed.Count);
    }

    return retVal;
}