Spiral Matrix and FSM (Finite State Machine)

Solution to this problem requires an FSM. The FSM controls the direction to which either the row or the column should move. Control the outer-loop based on the current list node. Time complexity then becomes 4 * 10^5. Code is down below, cheers, ACC.

Spiral Matrix IV - LeetCode

2326. Spiral Matrix IV

Medium

You are given two integers m and n, which represent the dimensions of a matrix.

You are also given the head of a linked list of integers.

Generate an m x n matrix that contains the integers in the linked list presented in spiral order (clockwise), starting from the top-left of the matrix. If there are remaining empty spaces, fill them with -1.

Return the generated matrix.

 

Example 1:

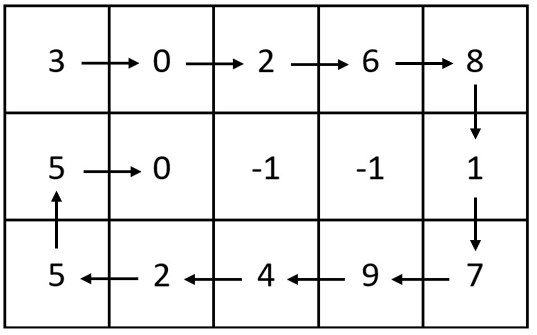
Input: m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
Output: [[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]
Explanation: The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.

Example 2:

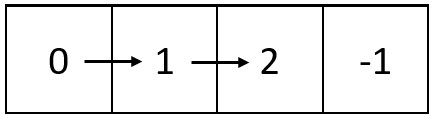
Input: m = 1, n = 4, head = [0,1,2]
Output: [[0,1,2,-1]]
Explanation: The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1.

 

Constraints:

• 1 <= m, n <= 105
• 1 <= m * n <= 105
• The number of nodes in the list is in the range [1, m * n].
• 0 <= Node.val <= 1000

public int[][] SpiralMatrix(int m, int n, ListNode head)
{
    int[][] matrix = new int[m][];

    for (int r = 0; r < m; r++)
    {
        matrix[r] = new int[n];
        for (int c = 0; c < n; c++)
        {
            matrix[r][c] = -1;
        }
    }

    char[] direction = new char[] { 'R', 'D', 'L', 'U' };
    int directionIndex = 0;
    int currentRow = 0;
    int currentCol = 0;
    ListNode node = head;

    while(node != null)
    {
        matrix[currentRow][currentCol] = node.val;
        node = node.next;

        int moveAttempts = 0;
        while (moveAttempts < direction.Length)
        {
            bool validMove = false;
            switch (direction[directionIndex])
            {
                case 'R':
                    if (currentCol + 1 < n && matrix[currentRow][currentCol + 1] == -1)
                    {
                        currentCol++;
                        validMove = true;
                    }
                    break;
                case 'D':
                    if (currentRow + 1 < m && matrix[currentRow + 1][currentCol] == -1)
                    {
                        currentRow++;
                        validMove = true;
                    }
                    break;
                case 'L':
                    if (currentCol - 1 >= 0 && matrix[currentRow][currentCol - 1] == -1)
                    {
                        currentCol--;
                        validMove = true;
                    }
                    break;
                case 'U':
                    if (currentRow - 1 >= 0 && matrix[currentRow - 1][currentCol] == -1)
                    {
                        currentRow--;
                        validMove = true;
                    }
                    break;
            }

            if (validMove) break;
            else
            {
                moveAttempts++;
                directionIndex = (directionIndex + 1) % direction.Length;
            }
        }

        if (moveAttempts == direction.Length) break;
    }

    return matrix;
}